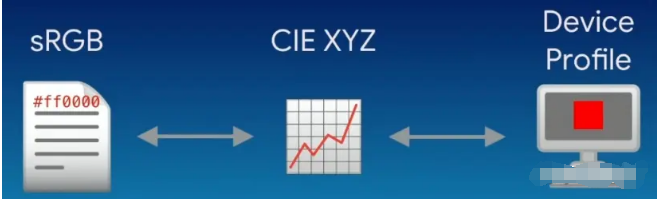
sRGB色彩空间是一种标准的RGB色彩空间，广泛应用于显示器、打印机以及因特网等领域。它将红、绿、蓝三原色的颜色定义为在CIE xy颜色坐标系中的特定位置，并通过非线性变换将原色强度与实际保存的数值之间进行转换。这种设计使得sRGB能够高效地表示人眼可以分辨的颜色。
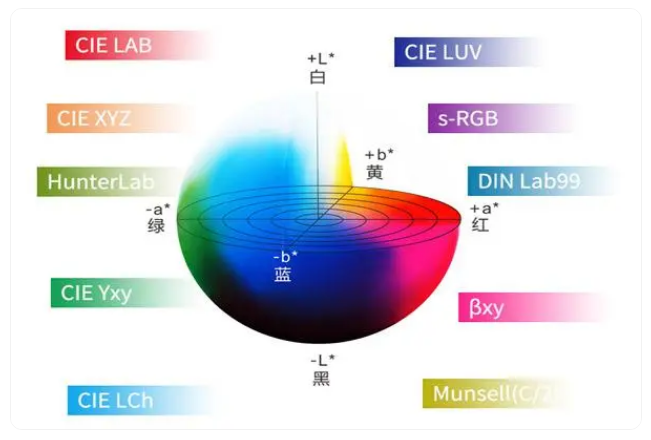
要将sRGB色彩空间中的RGB值转换为LAB值，需要进行一系列的计算。LAB色彩空间是一种基于人眼对颜色的感知而设计的色彩空间，其中L表示亮度，A和B表示色彩的两个维度。下面是一种常用的方法来进行RGB到LAB的转换：
1.将sRGB中的RGB值转换为线性RGB值。sRGB使用非线性变换来保存图像文件中的数值，因此需要将其逆变换为线性RGB值。这可以通过应用sRGB的逆gamma校正公式来实现。
2.将线性RGB值转换为XYZ值。XYZ色彩空间是一种与设备无关的色彩空间，可以作为RGB和LAB之间的桥梁。通过将线性RGB值乘以适当的转换矩阵，可以得到对应的XYZ值。
3.将XYZ值转换为LAB值。最后一步是将XYZ值转换为LAB值。这涉及到一些复杂的数学计算，包括对数函数和幂函数的运算。具体的转换公式可以在相关的色彩科学文献中找到。
需要注意的是，这些转换过程涉及到浮点数运算，因此在实际应用中可能需要进行适当的数值处理和近似计算。此外，色彩空间的转换也可能受到颜色管理系统的影响，因此在实际应用中可能需要根据特定的需求和标准进行调整和优化。
条条大路通罗马，就像我们可以用5+5来表示10，也可以用2x5来表示10，甚至是20-10也可，同样一种颜色，也可以用不同形式来表示。不同的形式有不同的优缺点，对于色彩空间来说，不同的空间能表示的色域是不同的。
用一个例子可以很好的理解不同的色彩空间以及他们之间的区别：假设有两个色彩空间，它们分别是R1 G1 B1和R2 G2 B2。现在我们的目标是，找到两个色彩空间之间的映射关系。现在我们已知R2 G2 B2 [1 0 0]的颜色情况，还有一个R1 G1 B1的显色器，若我把R1 G1 B1也设置成[1 0 0]，会出现这么个情况：（上标表示的是R1 G1 B1，下标表示的是R2 G2 B2）
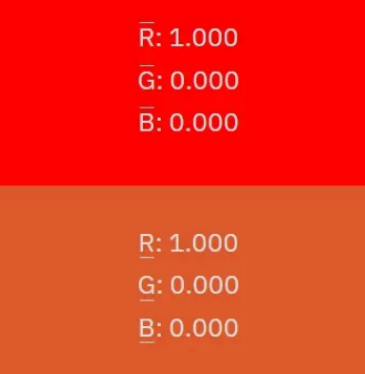
显然，这两个不同的色彩空间，那么通过调整R1 G1 B1，也可以使两种颜色一样，只不过确实要慢慢试：
那么根据此，我们可以得到以下的关系式：
R1 = R2 * 0.712
G1 = R2 * 0.100
B1 = R2 * 0.024
对R2 G2 B2 [0 1 0]和R2 G2 B2 [0 0 1]也是同理：
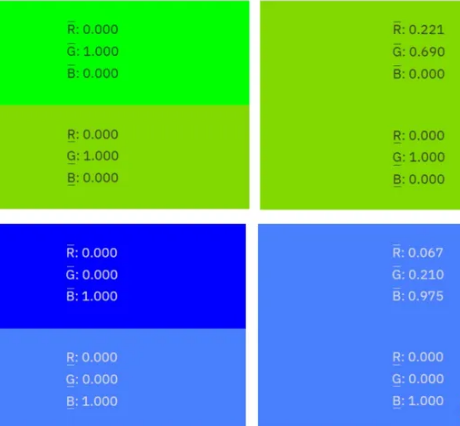
得到的关系式就分别是：
R1 = G2 * 0.221 ； R1 = B2 * 0.067
G1 = G2 * 0.690 ； G1 = B2 * 0.210
B1 = G2 * 0.000 ； B1 = B2 * 0.975
目前我们只知道R2 G2 B2为纯色的时候，R1 G1 B1分别要显示的量，那么如何确定非纯色的时候，R1 G1 B1要如何分配呢？比如说R2 G2 B2[0.9, 0.5, 0.2]的时候？
这个时候就要祭出我们的色觉尚方宝剑，格拉斯曼定律（Grassmann's laws），其内容是：人类对色彩的感知是线性的，即如果两个颜色的光匹配，此时添加另一组匹配的光，他们的总和也是匹配的。这里的匹配是指在一个色彩空间当中。
也就是说，我们已经知道R1 G1 B1分别与R2、G2、B2的关系，那么要求R1 G1 B1与R2 G2 B2的关系，我们只需要将其线性相加即可：
R1 = 0.712 * R2 + 0.221 * G2 + 0.067 * B2
G1 = 0.100 * R2 + 0.690 * G2 + 0.210 * B2
B1 = 0.024 * R2 + 0.000 * G2 + 0.976 * B2
那么我们解决上面的问题，当R2 G2 B2[0.9, 0.5, 0.2]时，把数值带入上式，得到其对应的R1 G1 B1为[0.765, 0.477, 0.217]，来验证一下：
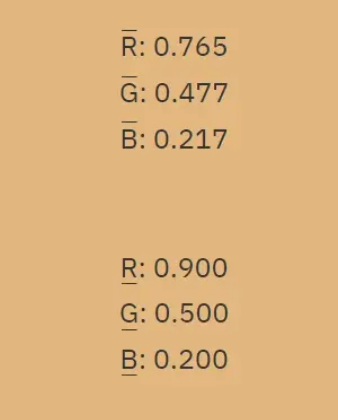
Amazing！我们再来进一步深入，那么假如我知道R1 G1 B1的值，要求R2 G2 B2对应值咋办呢，解一个三元一次方程也不是不行，我幼儿园的表弟也是这么想的。其实这里如果引入线性代数的知识，一切都会简单很多。
R1 G1 B1与R2 G2 B2的关系可以表示成：
那么根据小学二年级的线性代数知识，两边同时左乘A矩阵的逆，就可以得到：
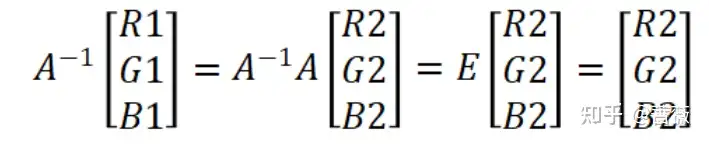
那么求出A矩阵的逆之后，不难得到：
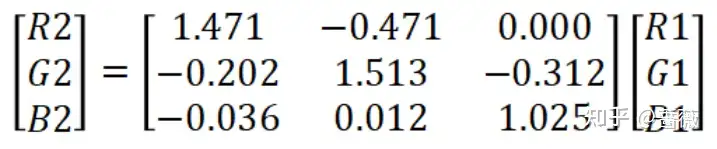
什么？你不会求矩阵的逆？哪里难了，有的时候找找自己的原因，这么多年了知识涨没涨，有没有认真学习（狗头
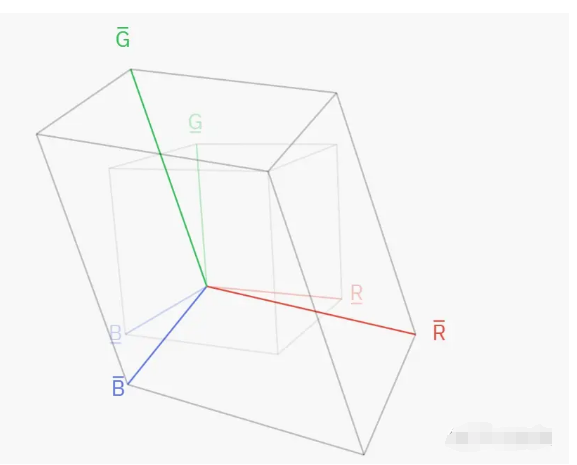
不废话，至此，运用了线性代数的知识后，我们不难发现，所谓不同的颜色空间之间的转换，无非就是向量基之间的转换罢了，我想这个概念应该学过线代的都很熟悉。那么如果把R1 G1 B1作为标准坐标系，绘制出的R2 G2 B2如图。并根据上面推出的关系绘制出的立体空间，空间内的任意一点都能表示一种颜色。那么显然，R1 G1 B1的立体空间更大，证明R1 G1 B1色彩空间中包含的颜色也会更多。
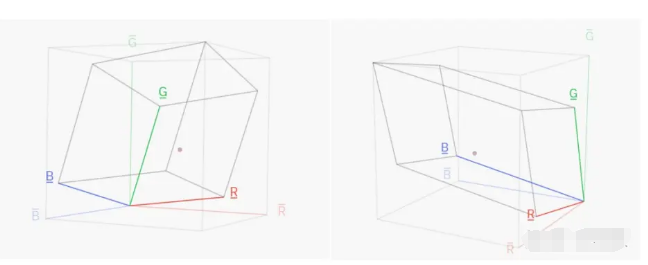
如果把R2 G2 B2作为标准坐标系，绘制出R1 G1 B1坐标系，得到的结论也是一样的：
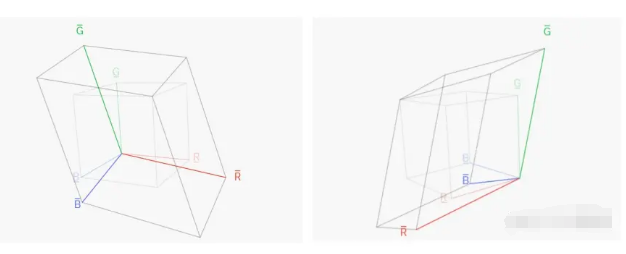
（如果觉得图很抽象看不懂，可以去这个网站里自己体验一下）
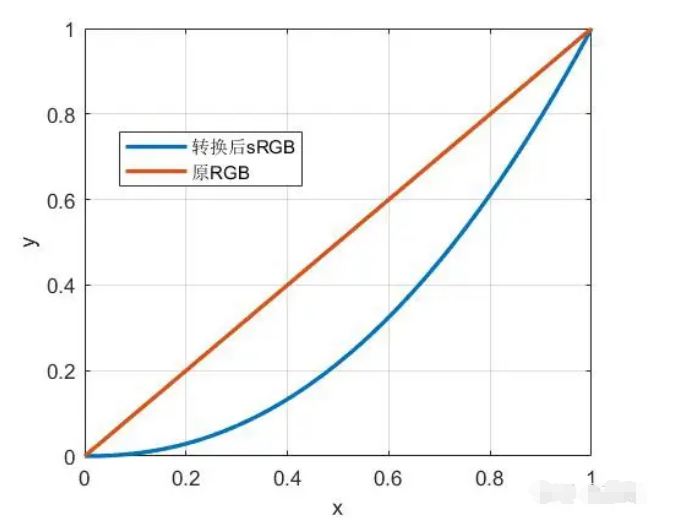
sRGB全称standard Red Green Blue，是一些影像巨头共同开发的一种彩色语言协议，其换算的公式本质就是一个γ值为2.2的gamma变换。至于为什么是2.2，这个和CRT（阴极射线管）显示器的工作原理相关了，不同的显示器gamma值也会不同，这里先按下不表。
gamma变换的公式为 ，如图：
若一个像素的RGB值（归一化后）为[0.1, 0.2, 0.3]，那么输出的sRGB就是[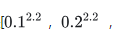
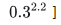简单易懂嗷兄弟们。
当然对此也有更深的理解，小学学过CV或者数字图像处理的同学应该知道，gamma变换通常与图像的对比度挂钩。当γ值大于1的时候，图像是整体变暗的。看起来和RGB没啥区别，那为什么好好的RGB不用，偏要整个sRGB出来呢？
这是因为我们人眼的视觉规律是非线性的，即人眼对暗域的变化更加敏感，下面来一个生动形象的例子：已知下面两张图最左边的色块和最右边的色块RGB分别为[0 0 0]和[255 255 255]，请问中间一部分的色块哪块最接近[128 128 128]？
我问了我身边的一些非相关专业的同学，基本都是选择了图一的左3和图二的第5个。如果结果和这个差不多朋友，恭喜你，你的眼睛是正常的。但是实际情况是什么？
如果非说要有个正确答案，那是图一的第5个和图二的右3。通过这个例子应该不难理解，人眼会觉得图一右侧的四张图亮度的差距会比左侧四张图的差距小，换句话说就是人眼对暗处的亮度变化更加敏感。而图二正是图一的RGB转成sRGB后的情况，所以人眼会觉得中间才是最接近[128 128 128]的，很好的证明了sRGB是符合人眼特性的。
XYZ是另一种表示颜色的方法，也叫三刺激值。在了解XYZ的由来以及含义前，非常有必要先知道，人眼是如何感知颜色的。目前大多人认可的是“阶段学说”，在人类的视网膜上有三种不同的感光锥体，因此可以使用三种颜色（但不是我们说的三原色RGB，至于为什么不是我下面解释）进行混加使得大脑呈现所有的颜色。当然混加也不是单纯的线性，而是一个复杂过程，这里有机会再深入学习一下（给自己挖个坑立个flag）。
重要的是，人类视觉系统的三色性，到底是哪三色？CIE为了探究这个答案，做了人眼色觉匹配实验，得到了如下图的结果。x轴是不同波长，y轴是归一化后的强度。
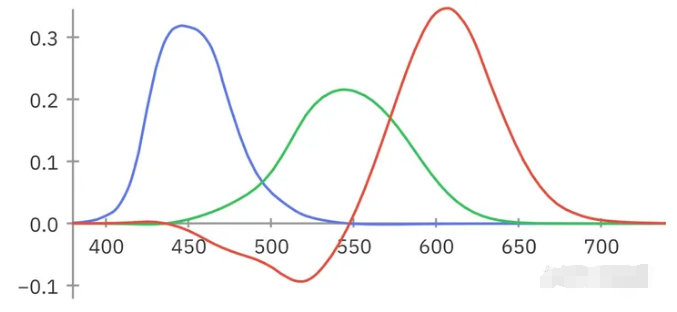
第一眼看这图，咋还有负数，这部瞎扯淡嘛，虚空的红？其实这就是为什么人类视觉系统的三色性中的三色（下面就简称三色）不是RGB的原因。
首先这张图的x坐标代表的是波长，在小学二年级的光学里我们就知道，对应于单一波长的颜色称为光谱颜色，也就是说，这个是我们定义颜色（无论在你脑子呈现的是什么颜色），例如波长为570nm的电磁波它就是纯黄色。这里有一点要注意，颜色之间没有一个硬性的界限，说过了这个波长它就是什么颜色，也就不存在单一的“光谱红色”。所以说了那么多p话，总结一句就是，如果把RGB作为三色，就会出现这样的负数问题证明普通RGB真不行。
我来举个例子：回顾一下我一开始举的两个色彩空间的例子，R1 G1 B1和R2 G2 B2，我们知道，R1 G1 B1色彩空间包含的颜色是比R2 G2 B2大的，那么如果R1 G1 B1为[1 0 0]，我怎么用R2 G2 B2来表示呢？你会发现，就算R2拉满，仍然不够红，如果把数据直接带到公式里面计算，则R2 G2 B2就为[1.471, -0.471, 0]。R2超出了1很好理解，就是R2 G2 B2颜色空间中的红不够嘛。这个负数就很抽象了，他与上面实验出现的负数有着异曲同工之妙。
上图是R2 G2 B2[1 0 0]和R1 G1 B1[1 0 0]，显然，左边是不够红的，但其实也可以理解成，右边是不够绿的，那么我们可以再右边加上一点绿，直至两边的颜色看起来相同，用式子能更直观：
1.0 * R1 + 0.0 * G1 + 0.0 * B1 = (TARGET) + 0.2 * G1
（我们随便假设是0.2吧，反正就是适量）
然后我们再将式子进行移项，也就可以得到：
1.0 * R1 + 0.0 * G1 + 0.0 * B1 - 0.2 * G1 = (TARGET)
通过阅读式子，我们可以知道，要想将左侧的颜色与右侧的目标颜色匹配，则需要在左边加上负量的绿光。从线性代数的知识也能理解，我们回顾以下这张图：
如果颜色点在R1 G1 B1和R2 G2 B2点内，那么不会出现负量的情况。但如果颜色点在R1 G1 B1内，在R2 G2 B2外，显然，R2 G2 B2一定会出现负数才能表示该颜色点。
当然，负量在现实世界上是无法做到的，就像XYZ一样（虽然XYZ色彩空间也不存在负量），不存在一个特定的颜色能表示XYZ或者说负量是没有实际物理意义的，但是很多的颜色空间都是数学模型，从数学上来说是完全可行的，只要我们最后再将这个色彩空间转换回物理显示器能显示的色彩空间（比如说sRGB）就可以了。实际上图像的传输也确实是这个流程。
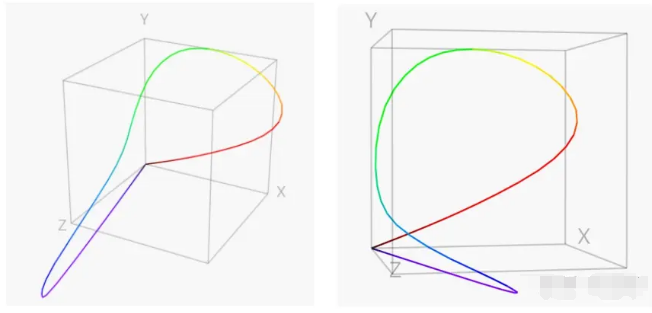
我们回到正题，CIE将实验的R光波长定为为700.0 nm，G光为546.1 nm，B光为435.8 nm。我以570 nm作为例子，从颜色匹配图中可以看出，匹配570nm对应的颜色需要 0.16768 个单位的 R、0.17087 个单位的 G 和 -0.00135 个单位的 B。一组三个 RGB 坐标可以表示成一个三位的坐标，那么把所有的颜色都绘制在一个三维的坐标系上，可以得到下图的结果：
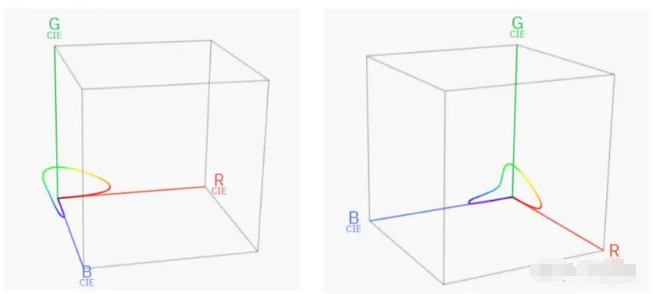
一条优美的曲线！只不过有负量存在，那么为了将这个“人眼色觉”空间转化成一个合理的色彩空间（这里的合理一是指没有负量，二是指将色度和亮度分离），CIE创建了以下方程组：
X = 2.769×R + 1.752×G + 1.130×B
Y = 1.000×R + 4.591×G + 0.061×B
Z = 0.000×R + 0.057×G + 5.594×B
其中Y分量是亮度分量，而 X 和 Z 定义色度。
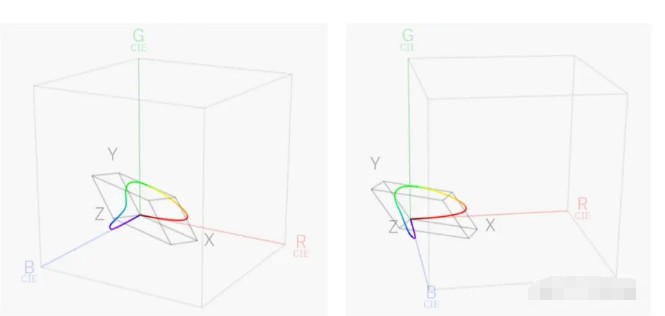
把XYZ作为直角坐标系，能更直观的看出这个色彩空间是合理的（主要是没有负量）。
至此，咱们就有一个基准颜色空间了，即任意两个色彩空间，我们现在不需要知道他们之间是如何转换的，只需要能够将它们都转换到 XYZ 空间就行了。
BLF 保来发